Waveform Introduction

Sound waves travel from a vibrating object – a musical instrument for instance, through a propagation medium – air – and make other objects vibrate – your body –. Air is a common propagation medium, but water and solids are also propagation mediums.

A soundwave is constitued of a succesion of compressions and rarefactions of air molecules.

• A vibrating object continually compresses and stretches the air around it.

• 

Compression is a region of increased pressure and rarefaction is region of decreased pressure.

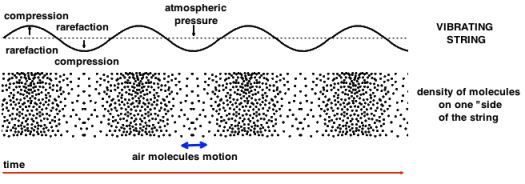
The sound wave propagation in space is incremental : a molecule oscillates in a longitudinal plane, around a rest position, and transmits its energy to the next molecule, and so on.

The waveform representation renders the compression and rarefaction of air molecules.

The amplitude of a soundwave corresponds to an air pressure expressed in Pascals (Pa). The atmospheric pressure is the reference value for 0 Pa.

The representation of the pressure variation is supposedely symetrical, since a compression of n Pa leads to a rarefaction of n Pa.

Here are a few milestones :

Schematically, sound waves propagate uniformly in all directions, as in a sphere. The loudness of the noise depends only on the distance between the receptor, and the source.

The intensity (I) of a sound wave is the amount of power (P) in the wave per unit area. It is the ratio of the sound power to the surface area of a sphere of radius r (surface area of sphere = 4π.r²). R is the distance from the sound source.

Power is expressed in Watts, intensity is expressed in Watts/m².

I = P / (4π.r²)

Just noticable differences of perceived qualities are generally relative, this is why we talk about perception levels. The physical intensity or pressure of a sound wave is different from the human perception of its intensity. The Weber–Fechner law describes the relationship between the physical magnitude of a stimuli and the perceived intensity of the stimuli.

This law is expressed S=k*log(I)

• where S = sensation, I = intensity, k = a given factor

• K depends on the type of sensation and physical magnitude.

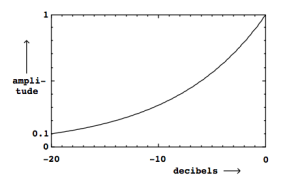
In the domain of acoustics, the decibel is a logarithmic unit that indicates the ratio of the physical intensity of a sound, relatively to a reference value. If sound pressure is represented in db the reference value is often the audibility threshold. For sound signal representation in AudioSculpt the reference value is full scale of the audio signal, that is the maximum amplitude that can be represented without cipping. Therefore in AudioSculpt all db values are negative. The dB unit allows to characterize the way the physical intensity, the sound pressure or the signal amplitude of a sound is perceived. Because dBs values are ratios they are a dimensionless quantities.

Perceived intensity can be calculated from an amount of physical pressure or an intensity. It is calculated from the base 10 logarithm of the pressure or intensity ratio of a value and a reference value. Base 10 logarithm is expressed "Log10".

What is a logarithm ?^[1]

L_P = Sound Pressure Level in dB, P = Pressure in Pa. As dBs are a relative quantity, we need a reference value : P⁰ which represents the audibility threshold. We get :

L_P (dB) = 20 * log10 (P/P₀).

If we apply this to the intensity of the spoken voice and threshold, relatively to air pressure, we get :

L = 20 * log10(50/0,02)

L = 20 * 3, 39794

L ≃ 68

To get information about logarithm calculus : see (french) (english).

L_I = Sound Intensity Level in dB, I =Intensity in W/m². The reference intensity value for the audibility threshold is I₀ = 10^-12 W/m².

To calculate the perceived intensity from the physcial intensity in W/m², we get :

L_I (dB) = 10 * log10 ( I / I₀ )

L_P (dB) = 20 * log10 (P/P₀)

L_I (dB) = 10 * log10 ( I / I₀ )